Bond Yield To Maturity Python Script

Bond Yield To Maturity Python Script

When interested in buying bonds a term that often comes up is the definition of Yield To Maturity (YTM).

Yield to maturity (YTM) is the total return anticipated on a bond if the bond is held until the end of its lifetime. Yield to maturity is considered a long-term bond yield, but is expressed as an annual rate. In other words, it is the internal rate of return of an investment in a bond if the investor holds the bond until maturity and if all payments are made as scheduled. - Investopedia

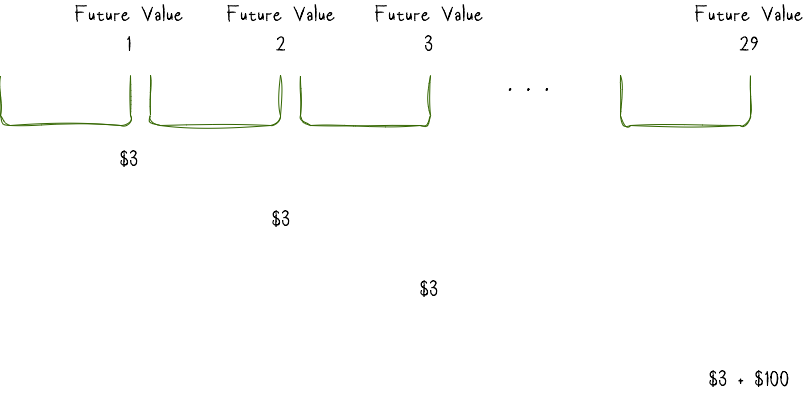
Let us consider a bond with a par value of \(\$100\) and a coupon rate of \(3\%\) with the bond maturing in \(29\) years time. The current bond price is \(\$89\). We are interested in the bond’s YTM.

Knowing that we get \(\$3\) annual cashflow (\(coupon\ rate \times par\ value = 0.03 \times \$100 = \$3\)) we will have the following cashflow for the next \(29\) years. Notice in the last year we will receive an additional \(\$100\) which is the bond’s principle:

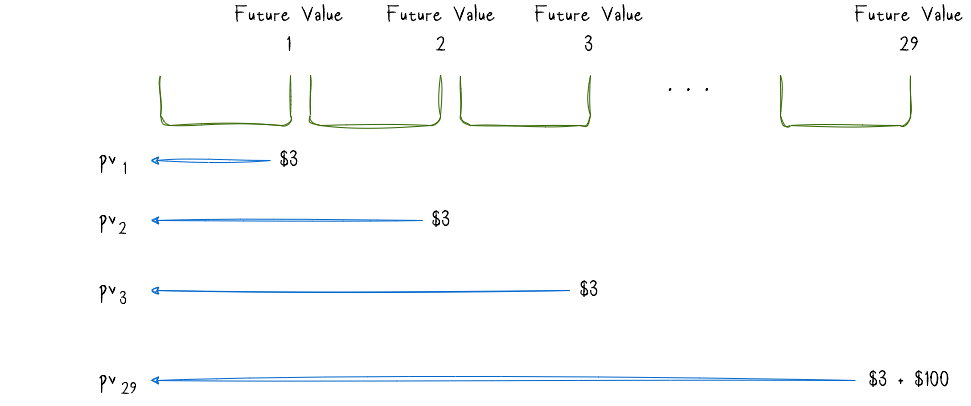
Let us assume that we want to value these future cashflows and determine how much they are worth today. What we need to do, is to present value all of these future cashflows back to today and add up those present values $ pv_i$. This sum would be the price of the bond.

A present value is the amount of money $ pv$ one would need to invest today in order to have \(c\) amount of money in \(n\) years if he is earning \(r\%\) annual interest on his investment:

$$ pv = \frac{c}{(1 + r)^n} $$

For example, if Bob wants to have \(\$100\) one year from now at a rate of \(5\%\), he needs to invest \(\$95.24\) today (\(\frac{100}{(1 + 0.05)} = 95.24\)), since:

$$ \$95.24 \times (1 + 0.05) \approx \$100. $$

Back to our bond’s present value of future cashflows the resulting formula would look as follows:

$$ bond\ price = \frac{future\ cashflow\ 1}{(1 + ytm)^1} + \frac{future\ cashflow\ 2}{(1 + ytm)^2} + \frac{future\ cashflow\ 3}{(1 + ytm)^3} + \dots + \frac{future\ cashflow\ 29}{(1 + ytm)^{29}} $$

with \(ytm\) being the yield to maturity we are looking for.

For our particular bond the formula will look like this:

$$ bond\ price = \frac{3}{(1 + ytm)^1} + \frac{3}{(1 + ytm)^2} + \frac{3}{(1 + ytm)^3} + \dots + \frac{3 + 100}{(1 + ytm)^{29}} $$

So how can we go about finding \(ytm\)? Well, above we have learned that sum of present values of all future cash flows is our bond price. Since we already know the today’s bond price which is \(\$89\), the formula becomes like this:

$$ \frac{3}{(1 + ytm)^1} + \frac{3}{(1 + ytm)^2} + \frac{3}{(1 + ytm)^3} + \dots + \frac{3 + 100}{(1 + ytm)^{29}} = 89 $$

All we need to do now is to solve the above equation for \(ytm\) so that it holds true. We will do this through trial-and-error.

Solving the equation by hand requires an understanding of the relationship between a bond’s price and its yield, as well as of the different types of bond pricings. Bonds can be priced at a discount, at par and at a premium. When the bond is priced at par, the bond’s interest rate is equal to its coupon rate. A bond priced above par (called a premium bond) has a coupon rate higher than the interest rate, and a bond priced below par (called a discount bond) has a coupon rate lower than the interest rate. So if an investor were calculating YTM on a bond priced below par, he or she would solve the equation by plugging in various annual interest rates that were higher than the coupon rate until finding a bond price close to the price of the bond in question (quote from: Investopedia).

You can verify this quickly with a simple example. Assume a bond with current price \(b\) and a par value of \(100\) that matures in \(1\) year. The coupon rate is \(c\) and interest rate is \(ytm\):

$$ b = \frac{100 + c \times 100}{(1 + ytm)} $$ $$ b \times (1 + ytm) = 100 + c \times 100 = 100 \times (1 + c) $$ $$ \frac{b}{100} = \frac{(1 + c)}{(1 + ytm)} $$

If \(\frac{b}{100} < 1\) then \((1 + ytm) > (1 + c)\). Similarly for the other cases.

Back to our bond. We had the following equation:

$$ \frac{3}{(1 + ytm)^1} + \frac{3}{(1 + ytm)^2} + \frac{3}{(1 + ytm)^3} + \dots + \frac{3 + 100}{(1 + ytm)^{29}} = 89 $$

Now we must solve for the interest rate \(ytm\) which is where things start to get difficult. Yet, we do not have to start simply guessing random numbers if we stop for a moment to consider the relationship between bond price and yield. As was mentioned above, when a bond is priced at a discount from par, its interest rate will be greater than the coupon rate. In this example, the par value of the bond is \(\$100\), but it is priced below the par value at \(\$89\), meaning that the bond is priced at a discount. As such, the annual interest rate we are seeking must necessarily be greater than the coupon rate of \(3\%\).

With this information we can now calculate and test a number of bond prices by plugging various annual interest rates that are higher than \(3\%\) into the formula above. Using a few different interest rates above \(3\%\), one would come up with the following bond prices:

...
ytm:3.61% price: 89.06
ytm:3.61% price: 89.04
ytm:3.61% price: 89.02
ytm:3.62% price: 89.01
ytm:3.62% price: 88.99

I have used \(0.00001\) increments and as we can see with an interest rate of \(3.62\%\) we can approximate our current price of \(\$89\) quite good enough. So \(3.62\%\) would be our Yield To Maturity.

$ python3 yield.py -p 139.87 -f 99.94 -r 6.250 -y 12 -s

The complete source code can be seen below:

import argparse
import math

def total_present_value(face_value, coupon, periods, rate):
    total_pv = 0
    for n in range(1, periods+1):
        total_pv += coupon / math.pow((1 + rate), n)

    total_pv += face_value / math.pow((1 + rate), periods)

    return total_pv


def main():
    """
    python3 yield.py -p 139.87 -f 99.94 -r 6.250 -y 12 -s
    """
    parser = argparse.ArgumentParser()
    parser.add_argument('-p', type=float, help='specifies the current price')
    parser.add_argument('-f', type=float, default=1000, help='specifies the face Value')
    parser.add_argument('-r', type=float, default=5, help='specifies the annual coupon rate in %')
    parser.add_argument('-y', type=int, default=15, help='specifies the number of years remaining to maturity')
    parser.add_argument('-s', action='store_true', default=False, help='coupon is a semi-annual coupon. Default is annual')
    args = parser.parse_args()

    coupon_rate = args.r / 100.0
    coupon = args.f * coupon_rate
    factor = 2 if args.s else 1

    print("------------------------------------------------")
    print("Price: %s" % args.p)
    print("Face Value: %s" % args.f)
    print("Annual coupon rate: %.2f%%" % args.r)
    print("Coupon: %s" % coupon)
    print("Semi-annual coupon: %s" % args.s)
    print("Years remaining: %s" % args.y)
    print("\n")


    ytm = coupon_rate
    condition = True
    while condition:
        if (args.p < args.f):
            ytm += 0.00001
        else:
            ytm -= 0.00001

        total_pv = total_present_value(args.f, coupon/factor, args.y*factor, ytm/factor)

        if (args.p < args.f):
            condition = total_pv > args.p
        else:
            condition = total_pv < args.p

    print("Yield to Maturity:  %.2f%%" % (ytm*100.0))


if __name__ == '__main__':
    main()

Price: 139.87
Face Value: 99.94
Annual coupon rate: 6.25%
Coupon: 6.24625
Semi-annual coupon: True
Years remaining: 12

Yield to Maturity: 2.40%