Implementing a Neural Network from Scratch in Python
Implementing a Neural Network from Scratch in Python
In this post, I will walk you through a step-by-step process for implementing a neural network entirely from scratch. Unlike most tutorials, which focus on using existing libraries like TensorFlow or Keras, this guide aims to show you how to build the foundational structure of a neural network itself—not simply how to use pre-built tools.
Today, the majority of engineers in organizations are skilled in using frameworks and libraries but may not fully understand how these tools are built. I believe that to truly excel as an engineer, one should develop the skills to create these tools as well. Sooner or later, when faced with complex challenges, you may find that existing frameworks do not fully meet your needs. At that point, the ability to engineer your own solution becomes invaluable. Otherwise, you’re just a user who configures and stitches together code that real engineers have written. Back in my day, we called that a script kiddie.
Think of the innovative tools we rely on today—ClickHouse, Keras, Pandas, Kafka, and many others. Each was created by someone who decided not only to use what others had built but to push the boundaries and create something new, more efficient, and better suited to their needs. This tutorial is for those who are ready to take that step and go beyond simply using established libraries.
I aim to make initializing a new neural network straightforward and accessible, following the simple steps outlined below:
1
2
3
4
5
6
7
8
9
10
11
12
def main():
topology = {
'input_layer_size': 1,
'number_of_hidden_layers': 1,
'hidden_layer_size': 3,
'output_layer_size': 1
}
net = Neural_Network(topology=topology)
if __name__ == "__main__":
main()
Model Serialization
The trained model (i.e. the weights) will be stored in a SQLite database. This allows us to avoid retraining the network every time it is needed, making it readily accessible and efficient to use.
Persistence
In this section, we will implement various helper functions that enable us to persist our model data to the database efficiently.
Let’s take a closer look at the constructor and how we set up our database.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Neural_Network(object):
def __init__(self, topology: Dict[str, int], db_name='nn.db', delete_old_db=False, reg_lambda=0.0001):
# Hyperparameters
self._number_of_hidden_layers = topology['number_of_hidden_layers']
self._input_layer_size = topology['input_layer_size']
self._hidden_layer_size = topology['hidden_layer_size']
self._output_layer_size = topology['output_layer_size']
self._LAMBDA = reg_lambda
if delete_old_db:
self._delete_database(db_name=db_name)
self._con = sqlite.connect(db_name)
self._setup_network()
################################################################################################
# PERSISTENCE
################################################################################################
def __del__(self):
self._con.close()
def _delete_database(self, db_name: str):
if os.path.exists(db_name):
os.remove(db_name)
def _setup_network(self):
self._TABLE_STANDARDIZATION_PARAMETERS = 'standardization'
self._TABLE_NAME_PREFIX = 'layer_'
self._TABLE_NAME_FOR_LAYER = {}
self._TABLE_NAME_WEIGHT_FOR_LAYERS = {}
self._TABLE_NAME_BIAS_FOR_LAYERS = {}
self._WEIGHTS_FOR_LAYER = {}
self._BIAS_FOR_LAYER = {}
self._OUTPUT_FOR_LAYER = {}
# Input Nodes
self._TABLE_NAME_FOR_LAYER[0] = f'{self._TABLE_NAME_PREFIX}input'
# Output Nodes
self._TABLE_NAME_FOR_LAYER[self._number_of_hidden_layers+1] = f'{self._TABLE_NAME_PREFIX}output'
# Hidden Layers
for l in range(1, self._number_of_hidden_layers+1):
self._TABLE_NAME_FOR_LAYER[l] = f'{self._TABLE_NAME_PREFIX}hidden_{l}'
# Weight Tables
for l in sorted(self._TABLE_NAME_FOR_LAYER.keys())[:-1]:
self._TABLE_NAME_WEIGHT_FOR_LAYERS[l] = f'weights_{self._TABLE_NAME_FOR_LAYER[l]}_to_{self._TABLE_NAME_FOR_LAYER[l+1]}'
self._TABLE_NAME_BIAS_FOR_LAYERS[l] = f'bias_to_{self._TABLE_NAME_FOR_LAYER[l+1]}'
self._create_tables()
for from_layer in sorted(self._TABLE_NAME_FOR_LAYER.keys())[:-1]:
to_layer = from_layer + 1
from_ids = self._fetch_all_ids_from_table(table=self._TABLE_NAME_FOR_LAYER[from_layer])
to_ids = self._fetch_all_ids_from_table(table=self._TABLE_NAME_FOR_LAYER[to_layer])
# Load weights from db
self._WEIGHTS_FOR_LAYER[from_layer] = np.array([[self._fetch_weight_from_db(r, c, from_layer) for c in to_ids] for r in from_ids])
self._BIAS_FOR_LAYER[from_layer] = np.array([[self._fetch_bias_from_db(c, from_layer) for c in to_ids]])
I won’t delve too deeply here, as the code is fairly self-explanatory. Essentially, each layer’s neuron IDs, the weights connecting neurons between layers, and the biases will be stored in separate, clearly labeled tables within the database for easy reference and organization.
Here is the implementation of the _create_tables() method:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
def _create_tables(self):
self._TABLE_COLUMN_MEAN_PREFIX = 'mean_'
self._TABLE_COLUMN_STD_PREFIX = 'std_'
self._TABLE_COLUMN_ID = 'id'
self._TABLE_COLUMN_FROM_ID = 'from_id'
self._TABLE_COLUMN_TO_ID = 'to_id'
self._TABLE_COLUMN_WEIGHT = 'weight'
self._TABLE_COLUMN_TYPE = 'type'
# Mean and Standard deviation table
columns = "("
columns += f"{self._TABLE_COLUMN_ID} INTEGER PRIMARY KEY,\n"
separator = ""
for i in range(self._input_layer_size):
columns += f"{separator}{self._TABLE_COLUMN_MEAN_PREFIX}{i} REAL, \n{self._TABLE_COLUMN_STD_PREFIX}{i} REAL"
separator = ",\n"
columns += ")"
self._con.execute(f"CREATE TABLE IF NOT EXISTS {self._TABLE_STANDARDIZATION_PARAMETERS} {columns}")
self._con.commit()
for layer in self._TABLE_NAME_FOR_LAYER:
table = self._TABLE_NAME_FOR_LAYER[layer]
self._con.execute(
f'''CREATE TABLE IF NOT EXISTS {table}
(
{self._TABLE_COLUMN_ID} INTEGER PRIMARY KEY
)'''
)
self._con.commit()
self._generate_and_persist_layer_nodes_to_db()
# Weight Tables
for from_layer in sorted(self._TABLE_NAME_FOR_LAYER.keys())[:-1]:
to_layer = from_layer + 1
from_table = self._TABLE_NAME_FOR_LAYER[from_layer]
to_table = self._TABLE_NAME_FOR_LAYER[to_layer]
weight_table = self._TABLE_NAME_WEIGHT_FOR_LAYERS[from_layer]
self._con.execute(
f'''CREATE TABLE IF NOT EXISTS {weight_table}
(
{self._TABLE_COLUMN_ID} INTEGER PRIMARY KEY,
{self._TABLE_COLUMN_FROM_ID} INTEGER,
{self._TABLE_COLUMN_TO_ID} INTEGER,
{self._TABLE_COLUMN_WEIGHT} REAL,
FOREIGN KEY({self._TABLE_COLUMN_FROM_ID}) REFERENCES {from_table}({self._TABLE_COLUMN_ID}),
FOREIGN KEY({self._TABLE_COLUMN_TO_ID}) REFERENCES {to_table}({self._TABLE_COLUMN_ID}),
UNIQUE({self._TABLE_COLUMN_FROM_ID}, {self._TABLE_COLUMN_TO_ID})
)'''
)
self._con.commit()
for from_layer in sorted(self._TABLE_NAME_FOR_LAYER.keys())[:-1]:
to_layer = from_layer + 1
bias_table = self._TABLE_NAME_BIAS_FOR_LAYERS[from_layer]
to_table = self._TABLE_NAME_FOR_LAYER[to_layer]
self._con.execute(
f'''CREATE TABLE IF NOT EXISTS {bias_table}
(
{self._TABLE_COLUMN_ID} INTEGER PRIMARY KEY,
{self._TABLE_COLUMN_TO_ID} INTEGER,
{self._TABLE_COLUMN_WEIGHT} REAL,
FOREIGN KEY({self._TABLE_COLUMN_TO_ID}) REFERENCES {to_table}({self._TABLE_COLUMN_ID}),
UNIQUE({self._TABLE_COLUMN_TO_ID})
)'''
)
self._con.commit()
self._generate_and_persist_synapses_to_db()
We will also let the database to automatically generate and populate the layer tables with IDs for each neuron in our network with the help of the _generate_and_persist_layer_nodes_to_db() method.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def _generate_and_persist_layer_nodes_to_db(self):
for layer in sorted(self._TABLE_NAME_FOR_LAYER.keys()):
table = self._TABLE_NAME_FOR_LAYER[layer]
ids = self._fetch_all_ids_from_table(table=table)
if len(ids) == 0:
if layer == 0:
number_of_nodes = self._input_layer_size
elif layer == self._number_of_hidden_layers+1:
number_of_nodes = self._output_layer_size
else:
number_of_nodes = self._hidden_layer_size
for _ in range(number_of_nodes):
cur = self._con.execute(
f"""
INSERT INTO {table} DEFAULT VALUES;
"""
)
self._con.commit()
We also store the initial weights and biases using the _generate_and_persist_synapses_to_db() function. For the input layer, the initial weight and bias are set to $\frac{1}{Number\ of\ Hidden\ Layers}$ for the input layer, while all other layers are initialized with a value of 1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
def _generate_and_persist_synapses_to_db(self):
for from_layer in sorted(self._TABLE_NAME_FOR_LAYER.keys())[:-1]:
to_layer = from_layer + 1
from_table = self._TABLE_NAME_FOR_LAYER[from_layer]
to_table = self._TABLE_NAME_FOR_LAYER[to_layer]
weight_table = self._TABLE_NAME_WEIGHT_FOR_LAYERS[from_layer]
bias_table = self._TABLE_NAME_BIAS_FOR_LAYERS[from_layer]
from_ids = self._fetch_all_ids_from_table(table=from_table)
to_ids = self._fetch_all_ids_from_table(table=to_table)
initial_weight = 1.0 / self._hidden_layer_size if from_layer == 0 else 1
for from_id in from_ids:
for to_id in to_ids:
cur = self._con.execute(
f"""
INSERT OR IGNORE INTO {weight_table}
(
{self._TABLE_COLUMN_FROM_ID},
{self._TABLE_COLUMN_TO_ID},
{self._TABLE_COLUMN_WEIGHT}
)
VALUES
(
{from_id},
{to_id},
{initial_weight}
)
"""
)
self._con.commit()
for to_id in to_ids:
cur = self._con.execute(
f"""
INSERT OR IGNORE INTO {bias_table}
(
{self._TABLE_COLUMN_TO_ID},
{self._TABLE_COLUMN_WEIGHT}
)
VALUES
(
{to_id},
{initial_weight}
)
"""
)
self._con.commit()
Let’s also define a few functions that will allow us to update the weights, bias and other parameter values in the database.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def _update_db_weights_and_bias(self):
for layer in sorted(self._WEIGHTS_FOR_LAYER.keys()):
W = self._WEIGHTS_FOR_LAYER[layer]
rows, columns = W.shape
for row in range(rows):
for col in range(columns):
self._persist_weight_to_db(from_id=row+1, to_id=col+1, from_layer=layer, weight=W[row][col])
for layer in sorted(self._BIAS_FOR_LAYER.keys()):
b = self._BIAS_FOR_LAYER[layer]
rows, columns = b.shape
for row in range(rows):
for col in range(columns):
self._persist_bias_to_db(to_id=col+1, from_layer=layer, weight=b[row][col])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
def _persist_mean_std_to_db(self, mean, std):
table = self._TABLE_STANDARDIZATION_PARAMETERS
res = self._con.execute(
f'''
SELECT
{self._TABLE_COLUMN_ID}
FROM
{table}
'''
).fetchone()
if res:
row_id = res[0]
columns_update = ""
separator = ""
for i in range(self._input_layer_size):
columns_update += f"{separator}{self._TABLE_COLUMN_MEAN_PREFIX}{i}={mean[i]}, {self._TABLE_COLUMN_STD_PREFIX}{i}={std[i]}"
separator = ", "
self._con.execute(
f'''
UPDATE {table}
SET
{columns_update}
WHERE
{self._TABLE_COLUMN_ID}={row_id}
'''
)
else:
columns_insert = "("
separator = ""
for i in range(self._input_layer_size):
columns_insert += f"{separator}{self._TABLE_COLUMN_MEAN_PREFIX}{i}, {self._TABLE_COLUMN_STD_PREFIX}{i}"
separator = ", "
columns_insert += ")"
values_insert = "("
separator = ""
for i in range(self._input_layer_size):
values_insert += f"{separator}{mean[i]}, {std[i]}"
separator = ", "
values_insert += ")"
self._con.execute(
f'''
INSERT INTO {table}
{columns_insert}
VALUES
{values_insert}
'''
)
self._con.commit()
def _persist_weight_to_db(self, from_id, to_id, from_layer, weight):
table = self._TABLE_NAME_WEIGHT_FOR_LAYERS[from_layer]
res = self._con.execute(
f'''
SELECT
{self._TABLE_COLUMN_ID}
FROM
{table}
WHERE
{self._TABLE_COLUMN_FROM_ID}={from_id}
AND
{self._TABLE_COLUMN_TO_ID}={to_id}
'''
).fetchone()
row_id = res[0]
self._con.execute(
f'''
UPDATE {table}
SET
{self._TABLE_COLUMN_WEIGHT}={weight}
WHERE
{self._TABLE_COLUMN_ID}={row_id}
'''
)
self._con.commit()
def _persist_bias_to_db(self, to_id, from_layer, weight):
table = self._TABLE_NAME_BIAS_FOR_LAYERS[from_layer]
res = self._con.execute(
f'''
SELECT
{self._TABLE_COLUMN_ID}
FROM
{table}
WHERE
{self._TABLE_COLUMN_TO_ID}={to_id}
'''
).fetchone()
row_id = res[0]
self._con.execute(
f'''
UPDATE {table}
SET
{self._TABLE_COLUMN_WEIGHT}={weight}
WHERE
{self._TABLE_COLUMN_ID}={row_id}
'''
)
self._con.commit()
Fetching the Model From the Database
In this section, we will implement various helper functions that enable us to retrieve our model data from the database efficiently.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
def _fetch_weight_from_db(self, from_id, to_id, from_layer):
table = self._TABLE_NAME_WEIGHT_FOR_LAYERS[from_layer]
res = self._con.execute(
f'''
SELECT
{self._TABLE_COLUMN_WEIGHT}
FROM
{table}
WHERE
{self._TABLE_COLUMN_FROM_ID}={from_id}
AND
{self._TABLE_COLUMN_TO_ID}={to_id}
'''
).fetchone()
return res[0]
def _fetch_bias_from_db(self, to_id, from_layer):
table = self._TABLE_NAME_BIAS_FOR_LAYERS[from_layer]
res = self._con.execute(
f'''
SELECT
{self._TABLE_COLUMN_WEIGHT}
FROM
{table}
WHERE
{self._TABLE_COLUMN_TO_ID}={to_id}
'''
).fetchone()
return res[0]
def _fetch_mean_std_from_db(self):
table = self._TABLE_STANDARDIZATION_PARAMETERS
columns = ""
separator = ""
for i in range(self._input_layer_size):
columns += f"{separator}{self._TABLE_COLUMN_MEAN_PREFIX}{i}, {self._TABLE_COLUMN_STD_PREFIX}{i}"
separator = ", "
res = self._con.execute(
f'''
SELECT
{columns}
FROM
{table}
'''
).fetchone()
means = []
stds = []
if res:
for i in range(0, len(res), 2):
means.append(res[i])
stds.append(res[i+1])
mean = np.array((means), dtype=float)
std = np.array((stds), dtype=float)
return mean, std
def _fetch_all_ids_from_table(self, table: str):
result = set()
cur = self._con.execute(
f'''
SELECT
{self._TABLE_COLUMN_ID}
FROM
{table}
'''
)
for row in cur:
result.add(row[0])
return sorted(list(result))
The Forward Pass
Alright, now that we’ve slogged through the boring boilerplate, let’s get to the fun and mathematical core of our neural network.
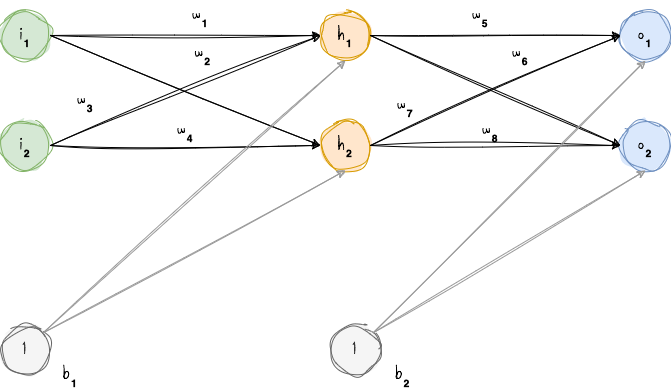
First, let’s illustrate the concept using a neural network with two input neurons, two hidden neurons, and two output neurons. Additionally, both the hidden and output neurons will include a bias term.
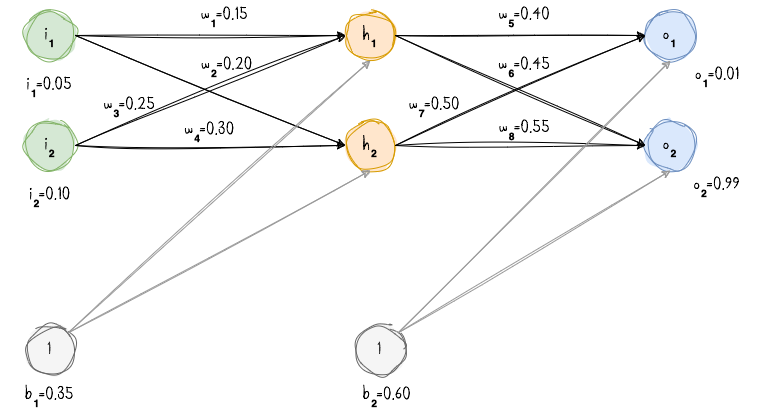
To provide a concrete example, here are the initial weights, biases, and training inputs/outputs:
To start, let’s examine the neural network’s current predictions using the weights and biases provided, with input values of $0.05$ and $0.10$. We’ll achieve this by feeding these inputs forward through the network. We want the neural network to produce outputs of $0.01$ and $0.99$.
First, we calculate the total net input for each neuron in the hidden layer, apply an activation function (here, standard logistic function) to squash the output, and then repeat the process for the neurons in the output layer:
\begin{align} \sigma(z) = \frac{1} {1 + e^{-z}} \end{align}
Let’s calculate the net input for the hidden layer neurons $h_1$ and $h_2$:
\begin{align} net_{h_1} = (i_1 \times w_1) + (i_2 \times w_2) + (b_1 \times 1) \end{align}
\begin{align} net_{h_1} = (0.5 \times 0.15) + (0.1 \times 0.2) + (0.35 \times 1) = 0.3775 \end{align}
We then apply the logistic function to squash the value, resulting in an output of:
\begin{align} out_{h_1} = \frac{1}{1 + e^{-net_{h_1}}} = \frac{1}{1 + e^{-0.3775}} = 0.593269992 \end{align}
Repeating the process for $h_2$ we get: \begin{align} out_{h_2} = 0.596884378 \end{align}
Next, we use the outputs from the hidden layer neurons as inputs to the neurons in the output layer.
\begin{align} net_{o_{1}} = (out_{h_{1}} \times w_5) + (w_6 \times out_{h_{2}}) + (b_2 \times 1) \end{align}
\begin{align} net_{o_{1}} = (0.593269992 \times 0.4) + (0.596884378 \times 0.45) + (0.6 \times 1) = 1.105905967 \end{align}
We then apply the logistic function to squash the value, resulting in an output of: \begin{align} out_{o_1} = \frac{1}{1 + e^{-net_{o_1}}} = \frac{1}{1 + e^{-1.105905967}} = 0.75136507 \end{align}
Repeating the process for $o_2$ we get: \begin{align} out_{o_2} = 0.772928465 \end{align}
Before we proceed, let’s define the Python method for our sigmoid function and its derivative:
1
2
3
4
5
def _sigmoid(self, z):
return 1/(1+np.exp(-z))
def _dsigmoid(self, z):
return np.exp(-z)/((1+np.exp(-z))**2)
Calculating the Total Error
We calculate the cost for each output neuron using the squared error function and then sum them to obtain the total error. One commonly used function is the mean squared error, which measures the difference between the actual value $y$ and the predicted value $\hat{y}$. This function quantifies how far off the predictions are from the actual values. \begin{align} J = \frac{1}{N}\times \sum_{}^{N} 0.5 \times (y - \hat{y})^2 + r \end{align}
The factor of $0.5$ is included so that the exponent is canceled when we differentiate later on. Ultimately, the result is multiplied by the learning rate, so introducing this constant doesn’t affect the outcome.
For example, if the target output $o_1$ is $0.01$ but the neural network’s output is $out_{o_1}=0.75136507$, if we ignore the regularization term $r$ for a moment, the error can be calculated as:
\begin{align} J_{out_{o_1}} = 0.5 \times (0.01 - 0.75136507)^2 = 0.27481108350805245 \end{align}
Repeating the process for $out_{o_2}$ we get: \begin{align} J_{out_{o_2}} = 0.5 \times (0.99 - 0.772928465)^2 = 0.02356002565362811 \end{align}
The total cost for the neural network is the sum of these errors: \begin{align} J = \frac{1}{N} \times (J_{out_{o_1}} + J_{out_{o_2}}) = \frac{1}{2} \times (0.274811 + 0.023560) = 0.1491855 \end{align}
Let’s define the Python method for our cost function:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def cost_function(self, X, y):
'''
Return cost given input X and known output y.
cost = 0.5 * sum((y - yHat)^2)/N + r
with:
N: number of samples
r: regularization
yHat: predicted output
'''
N = X.shape[0]
yHat = self.forward(X)
W = self._WEIGHTS_FOR_LAYER[0]
reg = np.sum(W**2)
for layer in sorted(self._WEIGHTS_FOR_LAYER.keys())[1:]:
W = self._WEIGHTS_FOR_LAYER[layer]
reg = reg + np.sum(W**2)
# We don't want cost to increase with the number of examples,
# so normalize by dividing the error term by number of examples(X.shape[0])
J = 0.5*sum((y-yHat)**2)/N + (self._LAMBDA/2)*reg
return J
The Backwards Pass
Our goal with backpropagation is to adjust each weight in the network so that the actual output moves closer to the target output, thereby minimizing the error for each output neuron and for the network as a whole.
Output Layer
This becomes clearer with an example. Consider the weight $w_5$. If we want to know how much a change in $w_5$ affects the total cost $J$ of the neural network, we can take the partial derivative of $J$ with respect to $w_5$ or the the gradient with respect to $w_5$:
\begin{align} \frac{ \partial J }{ \partial w_5 } \end{align}
We can then apply the chain rule to get:
\begin{align} \frac{ \partial J }{ \partial w_5 } = \frac{ \partial J }{ \partial out_{o_1} } \times \frac{ \partial out_{o_1} }{ \partial net_{o_1} } \times \frac{ \partial net_{o_1} }{ \partial w_5 } \end{align}
This concept is illustrated in the diagram below.
Remember:
\begin{align} J = \frac{1}{2} \times (0.5 \times (y_{o_1} - out_{o_1})^{2} + 0.5 \times (y_{o_2} - out_{o_2})^{2}) \end{align}
We need to break down each part of this equation. First, let’s determine how much the total cost changes with respect to the output.
\begin{align} \frac{ \partial J }{ \partial out_{o_1} } = \frac{1}{2} \times 2 \times 0.5 \times (y_{o_1} - out_{o_1})^{2-1} \times -1 + 0 = -\frac{1}{2} \times (y_{o_1} - out_{o_1}) \end{align} \begin{align} \frac{ \partial J }{ \partial out_{o_1} } = -\frac{1}{2} \times (0.01 - 0.75136507) = 0.370682535 \end{align}
Next, we need to calculate how much the output $out_{o_1} $changes with respect to its total net input $net_{o_1}$.
Remember: \begin{align} out_{o_1} = \frac{1}{1 + e^{-net_{o_1}}} \end{align} The partial derivative of the logistic function $\sigma(z)$ is given by: $\sigma(z) \times (1 - \sigma(z))$
\begin{align} \frac{ \partial out_{o_1} }{ \partial net_{o_1} } = out_{o_1} \times (1 - out_{o_1}) = 0.75136507 \times (1 - 0.75136507) = 0.186815602 \end{align}
The last term that we need to calculate is how much does the total net input of $o_1$ change with respect to $w_5$: $\frac{ \partial net_{o_1} }{ \partial w_5 }$
Remember: \begin{align} net_{o_{1}} = (out_{h_{1}} \times w_5) + (w_6 \times out_{h_{2}}) + (b_2 \times 1) \end{align} with: \begin{align} \frac{ \partial net_{o_1} }{ \partial w_5 } = out_{h_{1}} \times w_5^{1-1} + 0 + 0 = out_{h_{1}} = 0.593269992 \end{align}
Back to our original equation: \begin{align} \frac{ \partial J }{ \partial w_5 } = \frac{ \partial J }{ \partial out_{o_1} } \times \frac{ \partial out_{o_1} }{ \partial net_{o_1} } \times \frac{ \partial net_{o_1} }{ \partial w_5 } = 0.370682535 \times 0.186815602 \times 0.593269992 = 0.041083 \end{align}
What we are going to do now, and which can also been seen in our Python code later on is called the delta rule.
\begin{align} \frac{ \partial J }{ \partial w_5 } = \frac{ \partial J }{ \partial out_{o_1} } \times \frac{ \partial out_{o_1} }{ \partial net_{o_1} } \times \frac{ \partial net_{o_1} }{ \partial w_5 } = \delta_{o_1} \times \frac{ \partial net_{o_1} }{ \partial w_5 } = \delta_{o_1} \times out_{h_{1}} \end{align} with: \begin{align} \delta_{o_1} = -\frac{1}{2} \times (y_{o_1} - out_{o_1})\times out_{o_1} \times (1 - out_{o_1}) \end{align}
To reduce the error, we subtract this value from the current weight, optionally multiplying by a learning rate $\eta$ (which we’ll set to 0.5): \begin{align} w_{5}^{+} = w_{5} - \eta \times \frac{ \partial J }{ \partial w_5 } = 0.4 - 0.5\times 0.041083 = 0.3794585 \end{align}
We repeat the same process to calculate the updated weights $w_{6}^{+}$, $w_{7}^{+}$, $w_{8}^{+}$.
When continuing the backpropagation process into the hidden layer neurons, we use the original weights, not the updated ones.
Hidden Layer
We repeat the same process to calculate the updated weights of the hidden layer $w_{1}^{+}$, $w_{2}^{+}$, $w_{3}^{+}$ and $w_{4}^{+}$. Let us start with $w_{1}^{+}$. If we want to know how much a change in $w_1$ affects the total cost $J$ of the neural network, we can take the partial derivative of $J$ with respect to $w_1$:
\begin{align} \frac{ \partial J }{ \partial w_1 } = \frac{ \partial J }{ \partial out_{h_1} } \times \frac{ \partial out_{h_1} }{ \partial net_{h_1} } \times \frac{ \partial net_{h_1} }{ \partial w_1 } \end{align}
This concept is illustrated in the diagram below.
Now, let’s break down each term individually, starting with $\frac{ \partial J }{ \partial out_{h_1} }$.
We’ll follow a similar process as we did for the output layer, but with adjustments to account for the fact that each hidden layer neuron’s output contributes to the outputs (and thus the cost) of multiple output neurons. Since $out_{h_1}$ affects $out_{o_1}$ and $out_{o_2}$, we need to account for its impact on both output neurons when calculating $\frac{ \partial J }{ \partial out_{h_1} }$:
\begin{align} \frac{ \partial J }{ \partial out_{h_1} } = \frac{ \partial J_{o_1} }{ \partial out_{h_1}} + \frac{ \partial J_{o_2} }{ \partial out_{h_1}} \end{align}
with: \begin{align} \frac{ \partial J_{o_1} }{ \partial out_{h_1}} = \frac{ \partial J_{o_1} }{ \partial net_{o_1}} \times \frac{ \partial net_{o_1} }{ \partial out_{h_1}} \end{align}
\begin{align} \frac{ \partial J_{o_1} }{ \partial net_{o_1}} = \frac{ \partial J_{o_1} }{ \partial out_{o_1}} \times \frac{ \partial out_{o_1} }{ \partial net_{o_1}} = 0.370682535 \times 0.186815602 = 0.069249 \end{align}
Remember: \begin{align} net_{o_{1}} = (out_{h_{1}} \times w_5) + (w_6 \times out_{h_{2}}) + (b_2 \times 1) \end{align} which gives us: \begin{align} \frac{ \partial net_{o_1} }{ \partial out_{h_1}} = w_5 = 0.40 \end{align}
Thus we get: \begin{align} \frac{ \partial J_{o_1} }{ \partial out_{h_1}} = \frac{ \partial J_{o_1} }{ \partial net_{o_1}} \times \frac{ \partial net_{o_1} }{ \partial out_{h_1}} = 0.069249 \times 0.40 = 0.02769971237076443 \end{align}
We repeat the same process for $\frac{ \partial J_{o_2} }{ \partial out_{h_1}}$ and get $\frac{ \partial J_{o_2} }{ \partial out_{h_1}} = -0.10853576749999999$. Therefore: \begin{align} \frac{ \partial J }{ \partial out_{h_1} } = \frac{ \partial J_{o_1} }{ \partial out_{h_1}} + \frac{ \partial J_{o_2} }{ \partial out_{h_1}} = 0.0276997 - 0.1085357 = -0.08083605512923556 \end{align}
OK, now we have $\frac{ \partial J }{ \partial out_{h_1} }$. Let us continue with $\frac{ \partial out_{h_1} }{ \partial net_{h_1} }$. We know that: \begin{align} out_{h_1} = \frac{1}{1 + e^{-net_{h_1}}} = \frac{1}{1 + e^{-0.3775}} = 0.593269992 \end{align} This gives us: \begin{align} \frac{ \partial out_{h_1} }{ \partial net_{h_1} } = out_{h_1} \times (1 - out_{h_1}) = 0.593269992 \times (1 - 0.593269992) = 0.24130070859231995 \end{align}
Let us continue with the next term: $\frac{ \partial net_{h_1} }{ \partial w_1 }$. We know that: \begin{align} net_{h_1} = (i_1 \times w_1) + (i_2 \times w_2) + (b_1 \times 1) \end{align} Which gives us: \begin{align} \frac{ \partial net_{h_1} }{ \partial w_1 } = i_1 = 0.05 \end{align}
Plugging in all the terms for $\frac{ \partial J }{ \partial w_1 }$ we get: \begin{align} \frac{ \partial J }{ \partial w_1 } = \frac{ \partial J }{ \partial out_{h_1} } \times \frac{ \partial out_{h_1} }{ \partial net_{h_1} } \times \frac{ \partial net_{h_1} }{ \partial w_1 } = -0.0808360 \times 0.2413007 \times 0.05 = -0.000975289869124619 \end{align}
This can be rewritten in delta rule form: \begin{align} \frac{ \partial J }{ \partial w_1 } = ( \sum_{i}^{} \frac{ \partial J_{oi} }{ \partial out_{oi} } \times \frac{ \partial out_{oi} }{ \partial net_{oi} } \times \frac{ \partial net_{oi} }{ \partial out_{h_{1}} }) \times \frac{ \partial out_{h_1} }{ \partial net_{h_1} } \times \frac{ \partial net_{h_1} }{ \partial w_1 } \end{align}
\begin{align} \frac{ \partial J }{ \partial w_1 } = ( \sum_{i}^{} \delta_{oi} \times \frac{ \partial net_{oi} }{ \partial out_{h_{1}} }) \times out_{h_1} \times (1 - out_{h_1}) \times i_1 = ( \sum_{i}^{} \delta_{oi} \times w_{h_i}) \times out_{h_1} \times (1 - out_{h_1}) \times i_1 \end{align}
\begin{align} \frac{ \partial J }{ \partial w_1 } = \delta_{h_1} \times i_1 \end{align}
Finally we update $w_1$: \begin{align} w_{1}^{+} = w_{1} - \eta \times \frac{ \partial J }{ \partial w_1 } = 0.15 - (0.5\times -0.000975289869124619) = 0.1504876 \end{align} We repeat the same process to calculate the updated weights $w_{2}^{+}$, $w_{3}^{+}$, $w_{4}^{+}$.
With that, we’ve successfully updated all of our weights! Initially, when we fed forward inputs of $0.05$ and 0.1, the network’s error was $0.1491855$. After just one round of backpropagation, the error decreased slightly. Repeating this process $10,000$ times, for example, reduces the error dramatically to $0.0000351085$. At this point, feeding forward the inputs $0.05$ and $0.1$ produces outputs of $0.015$ (versus the target $0.01$) and $0.98$ (versus the target $0.99$).
Below are the Python functions for propagating inputs through the network, calculating derivatives, and performing gradient descent:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
def _derivatives_with_respect_to_weights(self, X, y):
N = X.shape[0]
dJdW_for_layer = {}
deltas_for_layer = {}
# Compute derivative with respect to W and W2 for a given X and y:
yHat = self.forward(X)
# Output Layer
W = self._WEIGHTS_FOR_LAYER[self._number_of_hidden_layers]
bias = self._BIAS_FOR_LAYER[self._number_of_hidden_layers]
net = np.dot(self._OUTPUT_FOR_LAYER[self._number_of_hidden_layers], W) + bias
# Compute the average gradient by dividing by sample size X.shape[0]. Also add gradient of regularization term.
deltas_for_layer[self._number_of_hidden_layers] = np.multiply(-(y - yHat), self._dsigmoid(net))
dJdW_for_layer[self._number_of_hidden_layers] = np.dot(self._OUTPUT_FOR_LAYER[self._number_of_hidden_layers].T, deltas_for_layer[self._number_of_hidden_layers])/N + self._LAMBDA*W
# Hidden Layers
for layer in sorted(self._TABLE_NAME_FOR_LAYER.keys(), reverse=True)[2:]:
W1 = self._WEIGHTS_FOR_LAYER[layer]
W2 = self._WEIGHTS_FOR_LAYER[layer + 1]
bias = self._BIAS_FOR_LAYER[layer]
net = np.dot(self._OUTPUT_FOR_LAYER[layer], W1) + bias
delta = deltas_for_layer[layer + 1]
deltas_for_layer[layer] = np.dot(delta, W2.T)*self._dsigmoid(net)
dJdW_for_layer[layer] = np.dot(self._OUTPUT_FOR_LAYER[layer].T, deltas_for_layer[layer])/N + self._LAMBDA*W1
return dJdW_for_layer, deltas_for_layer
# Gradient Descent
def train_using_gradient_descent(self, X, y, learning_rate=0.5):
'''
Train network using gradient descent.
'''
N = X.shape[0]
dJdW_for_layer, deltas_for_layer = self._derivatives_with_respect_to_weights(X, y)
for layer in sorted(self._WEIGHTS_FOR_LAYER.keys()):
W = self._WEIGHTS_FOR_LAYER[layer]
self._WEIGHTS_FOR_LAYER[layer] -= learning_rate * dJdW_for_layer[layer]
self._BIAS_FOR_LAYER[layer] -= learning_rate * np.sum(deltas_for_layer[layer], axis=0, keepdims=True)/N
self._update_db_weights_and_bias()
def forward(self, X):
'''
Propogate inputs though network.
'''
self._OUTPUT_FOR_LAYER[0] = X
for layer in sorted(self._TABLE_NAME_FOR_LAYER.keys())[1:]:
W = self._WEIGHTS_FOR_LAYER[layer - 1]
bias = self._BIAS_FOR_LAYER[layer - 1]
net = np.dot(self._OUTPUT_FOR_LAYER[layer - 1], W) + bias
self._OUTPUT_FOR_LAYER[layer] = self._sigmoid(net)
yHat = self._OUTPUT_FOR_LAYER[self._number_of_hidden_layers+1]
return yHat
In addition, the neural network includes helper functions for standardizing and min-max normalizing the $X$ and $y$ vectors.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def _standardize(self, X, y, persist=True):
'''
Standardizes X and y vectors and persists the input vector (X)
mean and standard deviation to the database for future use.
Procedure:
z=(X-μ)/std
1. Find mean (μ) and standard deviation for each feature or output vector.
2. Subtract mean (μ) from the samples (X) or output y.
3. Divide with standard deviation.
Returns standardized X and y vectors.
'''
mean, std = self._fetch_mean_std_from_db()
if mean.size == 0 and std.size == 0:
mean = np.mean(X, axis=0)
std = np.std(X, axis=0)
if persist:
self._persist_mean_std_to_db(mean, std)
X_std = (X-mean)/std
y_std = (y - np.mean(y, axis=0))/np.std(y, axis=0)
return X_std, y_std
def transform(self, X, y):
'''
Returns min-max normalized X and y vectors.
'''
X_scaled = (X - np.min(X, axis=0))/(np.max(X, axis=0) - np.min(X, axis=0))
y_scaled = (y - np.min(y, axis=0))/(np.max(y, axis=0) - np.min(y, axis=0))
return X_scaled, y_scaled
This concludes our neural network implementation. In the next post, I’ll cover how to train and test the network, and finally, how to use it for making predictions. The complete code is provided below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
import commons
import sqlite3 as sqlite
import numpy as np
from numpy import linalg as LA
import os
from typing import Dict
class Neural_Network(object):
def __init__(self, topology: Dict[str, int], db_name='nn.db', delete_old_db=False, reg_lambda=0.0001):
# Hyperparameters
self._number_of_hidden_layers = topology['number_of_hidden_layers']
self._input_layer_size = topology['input_layer_size']
self._hidden_layer_size = topology['hidden_layer_size']
self._output_layer_size = topology['output_layer_size']
self._LAMBDA = reg_lambda
if delete_old_db:
self._delete_database(db_name=db_name)
self._con = sqlite.connect(db_name)
self._setup_network()
################################################################################################
# PERSISTENCE
################################################################################################
def __del__(self):
self._con.close()
def _delete_database(self, db_name: str):
if os.path.exists(db_name):
os.remove(db_name)
def _setup_network(self):
self._TABLE_STANDARDIZATION_PARAMETERS = 'standardization'
self._TABLE_NAME_PREFIX = 'layer_'
self._TABLE_NAME_FOR_LAYER = {}
self._TABLE_NAME_WEIGHT_FOR_LAYERS = {}
self._TABLE_NAME_BIAS_FOR_LAYERS = {}
self._WEIGHTS_FOR_LAYER = {}
self._BIAS_FOR_LAYER = {}
self._OUTPUT_FOR_LAYER = {}
# Input Nodes
self._TABLE_NAME_FOR_LAYER[0] = f'{self._TABLE_NAME_PREFIX}input'
# Output Nodes
self._TABLE_NAME_FOR_LAYER[self._number_of_hidden_layers+1] = f'{self._TABLE_NAME_PREFIX}output'
# Hidden Layers
for l in range(1, self._number_of_hidden_layers+1):
self._TABLE_NAME_FOR_LAYER[l] = f'{self._TABLE_NAME_PREFIX}hidden_{l}'
# Weight Tables
for l in sorted(self._TABLE_NAME_FOR_LAYER.keys())[:-1]:
self._TABLE_NAME_WEIGHT_FOR_LAYERS[l] = f'weights_{self._TABLE_NAME_FOR_LAYER[l]}_to_{self._TABLE_NAME_FOR_LAYER[l+1]}'
self._TABLE_NAME_BIAS_FOR_LAYERS[l] = f'bias_to_{self._TABLE_NAME_FOR_LAYER[l+1]}'
self._create_tables()
for from_layer in sorted(self._TABLE_NAME_FOR_LAYER.keys())[:-1]:
to_layer = from_layer + 1
from_ids = self._fetch_all_ids_from_table(table=self._TABLE_NAME_FOR_LAYER[from_layer])
to_ids = self._fetch_all_ids_from_table(table=self._TABLE_NAME_FOR_LAYER[to_layer])
# Load weights from db
self._WEIGHTS_FOR_LAYER[from_layer] = np.array([[self._fetch_weight_from_db(r, c, from_layer) for c in to_ids] for r in from_ids])
self._BIAS_FOR_LAYER[from_layer] = np.array([[self._fetch_bias_from_db(c, from_layer) for c in to_ids]])
def _create_tables(self):
self._TABLE_COLUMN_MEAN_PREFIX = 'mean_'
self._TABLE_COLUMN_STD_PREFIX = 'std_'
self._TABLE_COLUMN_ID = 'id'
self._TABLE_COLUMN_FROM_ID = 'from_id'
self._TABLE_COLUMN_TO_ID = 'to_id'
self._TABLE_COLUMN_WEIGHT = 'weight'
self._TABLE_COLUMN_TYPE = 'type'
# Mean and Standard deviation table
columns = "("
columns += f"{self._TABLE_COLUMN_ID} INTEGER PRIMARY KEY,\n"
separator = ""
for i in range(self._input_layer_size):
columns += f"{separator}{self._TABLE_COLUMN_MEAN_PREFIX}{i} REAL, \n{self._TABLE_COLUMN_STD_PREFIX}{i} REAL"
separator = ",\n"
columns += ")"
self._con.execute(f"CREATE TABLE IF NOT EXISTS {self._TABLE_STANDARDIZATION_PARAMETERS} {columns}")
self._con.commit()
for layer in self._TABLE_NAME_FOR_LAYER:
table = self._TABLE_NAME_FOR_LAYER[layer]
self._con.execute(
f'''CREATE TABLE IF NOT EXISTS {table}
(
{self._TABLE_COLUMN_ID} INTEGER PRIMARY KEY
)'''
)
self._con.commit()
self._generate_and_persist_layer_nodes_to_db()
# Weight Tables
for from_layer in sorted(self._TABLE_NAME_FOR_LAYER.keys())[:-1]:
to_layer = from_layer + 1
from_table = self._TABLE_NAME_FOR_LAYER[from_layer]
to_table = self._TABLE_NAME_FOR_LAYER[to_layer]
weight_table = self._TABLE_NAME_WEIGHT_FOR_LAYERS[from_layer]
self._con.execute(
f'''CREATE TABLE IF NOT EXISTS {weight_table}
(
{self._TABLE_COLUMN_ID} INTEGER PRIMARY KEY,
{self._TABLE_COLUMN_FROM_ID} INTEGER,
{self._TABLE_COLUMN_TO_ID} INTEGER,
{self._TABLE_COLUMN_WEIGHT} REAL,
FOREIGN KEY({self._TABLE_COLUMN_FROM_ID}) REFERENCES {from_table}({self._TABLE_COLUMN_ID}),
FOREIGN KEY({self._TABLE_COLUMN_TO_ID}) REFERENCES {to_table}({self._TABLE_COLUMN_ID}),
UNIQUE({self._TABLE_COLUMN_FROM_ID}, {self._TABLE_COLUMN_TO_ID})
)'''
)
self._con.commit()
for from_layer in sorted(self._TABLE_NAME_FOR_LAYER.keys())[:-1]:
to_layer = from_layer + 1
bias_table = self._TABLE_NAME_BIAS_FOR_LAYERS[from_layer]
to_table = self._TABLE_NAME_FOR_LAYER[to_layer]
self._con.execute(
f'''CREATE TABLE IF NOT EXISTS {bias_table}
(
{self._TABLE_COLUMN_ID} INTEGER PRIMARY KEY,
{self._TABLE_COLUMN_TO_ID} INTEGER,
{self._TABLE_COLUMN_WEIGHT} REAL,
FOREIGN KEY({self._TABLE_COLUMN_TO_ID}) REFERENCES {to_table}({self._TABLE_COLUMN_ID}),
UNIQUE({self._TABLE_COLUMN_TO_ID})
)'''
)
self._con.commit()
self._generate_and_persist_synapses_to_db()
def _fetch_weight_from_db(self, from_id, to_id, from_layer):
table = self._TABLE_NAME_WEIGHT_FOR_LAYERS[from_layer]
res = self._con.execute(
f'''
SELECT
{self._TABLE_COLUMN_WEIGHT}
FROM
{table}
WHERE
{self._TABLE_COLUMN_FROM_ID}={from_id}
AND
{self._TABLE_COLUMN_TO_ID}={to_id}
'''
).fetchone()
return res[0]
def _fetch_bias_from_db(self, to_id, from_layer):
table = self._TABLE_NAME_BIAS_FOR_LAYERS[from_layer]
res = self._con.execute(
f'''
SELECT
{self._TABLE_COLUMN_WEIGHT}
FROM
{table}
WHERE
{self._TABLE_COLUMN_TO_ID}={to_id}
'''
).fetchone()
return res[0]
def _fetch_mean_std_from_db(self):
table = self._TABLE_STANDARDIZATION_PARAMETERS
columns = ""
separator = ""
for i in range(self._input_layer_size):
columns += f"{separator}{self._TABLE_COLUMN_MEAN_PREFIX}{i}, {self._TABLE_COLUMN_STD_PREFIX}{i}"
separator = ", "
res = self._con.execute(
f'''
SELECT
{columns}
FROM
{table}
'''
).fetchone()
means = []
stds = []
if res:
for i in range(0, len(res), 2):
means.append(res[i])
stds.append(res[i+1])
mean = np.array((means), dtype=float)
std = np.array((stds), dtype=float)
return mean, std
def _persist_mean_std_to_db(self, mean, std):
table = self._TABLE_STANDARDIZATION_PARAMETERS
res = self._con.execute(
f'''
SELECT
{self._TABLE_COLUMN_ID}
FROM
{table}
'''
).fetchone()
if res:
row_id = res[0]
columns_update = ""
separator = ""
for i in range(self._input_layer_size):
columns_update += f"{separator}{self._TABLE_COLUMN_MEAN_PREFIX}{i}={mean[i]}, {self._TABLE_COLUMN_STD_PREFIX}{i}={std[i]}"
separator = ", "
self._con.execute(
f'''
UPDATE {table}
SET
{columns_update}
WHERE
{self._TABLE_COLUMN_ID}={row_id}
'''
)
else:
columns_insert = "("
separator = ""
for i in range(self._input_layer_size):
columns_insert += f"{separator}{self._TABLE_COLUMN_MEAN_PREFIX}{i}, {self._TABLE_COLUMN_STD_PREFIX}{i}"
separator = ", "
columns_insert += ")"
values_insert = "("
separator = ""
for i in range(self._input_layer_size):
values_insert += f"{separator}{mean[i]}, {std[i]}"
separator = ", "
values_insert += ")"
self._con.execute(
f'''
INSERT INTO {table}
{columns_insert}
VALUES
{values_insert}
'''
)
self._con.commit()
def _persist_weight_to_db(self, from_id, to_id, from_layer, weight):
table = self._TABLE_NAME_WEIGHT_FOR_LAYERS[from_layer]
res = self._con.execute(
f'''
SELECT
{self._TABLE_COLUMN_ID}
FROM
{table}
WHERE
{self._TABLE_COLUMN_FROM_ID}={from_id}
AND
{self._TABLE_COLUMN_TO_ID}={to_id}
'''
).fetchone()
row_id = res[0]
self._con.execute(
f'''
UPDATE {table}
SET
{self._TABLE_COLUMN_WEIGHT}={weight}
WHERE
{self._TABLE_COLUMN_ID}={row_id}
'''
)
self._con.commit()
def _persist_bias_to_db(self, to_id, from_layer, weight):
table = self._TABLE_NAME_BIAS_FOR_LAYERS[from_layer]
res = self._con.execute(
f'''
SELECT
{self._TABLE_COLUMN_ID}
FROM
{table}
WHERE
{self._TABLE_COLUMN_TO_ID}={to_id}
'''
).fetchone()
row_id = res[0]
self._con.execute(
f'''
UPDATE {table}
SET
{self._TABLE_COLUMN_WEIGHT}={weight}
WHERE
{self._TABLE_COLUMN_ID}={row_id}
'''
)
self._con.commit()
def _fetch_all_ids_from_table(self, table: str):
result = set()
cur = self._con.execute(
f'''
SELECT
{self._TABLE_COLUMN_ID}
FROM
{table}
'''
)
for row in cur:
result.add(row[0])
return sorted(list(result))
def _generate_and_persist_layer_nodes_to_db(self):
for layer in sorted(self._TABLE_NAME_FOR_LAYER.keys()):
table = self._TABLE_NAME_FOR_LAYER[layer]
ids = self._fetch_all_ids_from_table(table=table)
if len(ids) == 0:
if layer == 0:
number_of_nodes = self._input_layer_size
elif layer == self._number_of_hidden_layers+1:
number_of_nodes = self._output_layer_size
else:
number_of_nodes = self._hidden_layer_size
for _ in range(number_of_nodes):
cur = self._con.execute(
f"""
INSERT INTO {table} DEFAULT VALUES;
"""
)
self._con.commit()
def _generate_and_persist_synapses_to_db(self):
for from_layer in sorted(self._TABLE_NAME_FOR_LAYER.keys())[:-1]:
to_layer = from_layer + 1
from_table = self._TABLE_NAME_FOR_LAYER[from_layer]
to_table = self._TABLE_NAME_FOR_LAYER[to_layer]
weight_table = self._TABLE_NAME_WEIGHT_FOR_LAYERS[from_layer]
bias_table = self._TABLE_NAME_BIAS_FOR_LAYERS[from_layer]
from_ids = self._fetch_all_ids_from_table(table=from_table)
to_ids = self._fetch_all_ids_from_table(table=to_table)
initial_weight = 1.0 / self._hidden_layer_size if from_layer == 0 else 1
for from_id in from_ids:
for to_id in to_ids:
cur = self._con.execute(
f"""
INSERT OR IGNORE INTO {weight_table}
(
{self._TABLE_COLUMN_FROM_ID},
{self._TABLE_COLUMN_TO_ID},
{self._TABLE_COLUMN_WEIGHT}
)
VALUES
(
{from_id},
{to_id},
{initial_weight}
)
"""
)
self._con.commit()
for to_id in to_ids:
cur = self._con.execute(
f"""
INSERT OR IGNORE INTO {bias_table}
(
{self._TABLE_COLUMN_TO_ID},
{self._TABLE_COLUMN_WEIGHT}
)
VALUES
(
{to_id},
{initial_weight}
)
"""
)
self._con.commit()
def _update_db_weights_and_bias(self):
for layer in sorted(self._WEIGHTS_FOR_LAYER.keys()):
W = self._WEIGHTS_FOR_LAYER[layer]
rows, columns = W.shape
for row in range(rows):
for col in range(columns):
self._persist_weight_to_db(from_id=row+1, to_id=col+1, from_layer=layer, weight=W[row][col])
for layer in sorted(self._BIAS_FOR_LAYER.keys()):
b = self._BIAS_FOR_LAYER[layer]
rows, columns = b.shape
for row in range(rows):
for col in range(columns):
self._persist_bias_to_db(to_id=col+1, from_layer=layer, weight=b[row][col])
################################################################################################
# LEARNING & TRAINING
################################################################################################
def _sigmoid(self, z):
return 1/(1+np.exp(-z))
def _dsigmoid(self, z):
return np.exp(-z)/((1+np.exp(-z))**2)
def _derivatives_with_respect_to_weights(self, X, y):
N = X.shape[0]
dJdW_for_layer = {}
deltas_for_layer = {}
# Compute derivative with respect to W and W2 for a given X and y:
yHat = self.forward(X)
# Output Layer
W = self._WEIGHTS_FOR_LAYER[self._number_of_hidden_layers]
bias = self._BIAS_FOR_LAYER[self._number_of_hidden_layers]
net = np.dot(self._OUTPUT_FOR_LAYER[self._number_of_hidden_layers], W) + bias
# Compute the average gradient by dividing by sample size X.shape[0]. Also add gradient of regularization term.
deltas_for_layer[self._number_of_hidden_layers] = np.multiply(-(y - yHat), self._dsigmoid(net))
dJdW_for_layer[self._number_of_hidden_layers] = np.dot(self._OUTPUT_FOR_LAYER[self._number_of_hidden_layers].T, deltas_for_layer[self._number_of_hidden_layers])/N + self._LAMBDA*W
# Hidden Layers
for layer in sorted(self._TABLE_NAME_FOR_LAYER.keys(), reverse=True)[2:]:
W1 = self._WEIGHTS_FOR_LAYER[layer]
W2 = self._WEIGHTS_FOR_LAYER[layer + 1]
bias = self._BIAS_FOR_LAYER[layer]
net = np.dot(self._OUTPUT_FOR_LAYER[layer], W1) + bias
delta = deltas_for_layer[layer + 1]
deltas_for_layer[layer] = np.dot(delta, W2.T)*self._dsigmoid(net)
dJdW_for_layer[layer] = np.dot(self._OUTPUT_FOR_LAYER[layer].T, deltas_for_layer[layer])/N + self._LAMBDA*W1
return dJdW_for_layer, deltas_for_layer
def cost_function(self, X, y):
'''
Return cost given input X and known output y.
cost = 0.5 * sum((y - yHat)^2)/N + r
with:
N: number of samples
r: regularization
yHat: predicted output
'''
N = X.shape[0]
yHat = self.forward(X)
W = self._WEIGHTS_FOR_LAYER[0]
reg = np.sum(W**2)
for layer in sorted(self._WEIGHTS_FOR_LAYER.keys())[1:]:
W = self._WEIGHTS_FOR_LAYER[layer]
reg = reg + np.sum(W**2)
# We don't want cost to increase with the number of examples,
# so normalize by dividing the error term by number of examples(X.shape[0])
J = 0.5*sum((y-yHat)**2)/N + (self._LAMBDA/2)*reg
return J
def _standardize(self, X, y, persist=True):
'''
Standardizes X and y vectors and persists the input vector (X)
mean and standard deviation to the database for future use.
Procedure:
z=(X-μ)/std
1. Find mean (μ) and standard deviation for each feature or output vector.
2. Subtract mean (μ) from the samples (X) or output y.
3. Divide with standard deviation.
Returns standardized X and y vectors.
'''
mean, std = self._fetch_mean_std_from_db()
if mean.size == 0 and std.size == 0:
mean = np.mean(X, axis=0)
std = np.std(X, axis=0)
if persist:
self._persist_mean_std_to_db(mean, std)
X_std = (X-mean)/std
y_std = (y - np.mean(y, axis=0))/np.std(y, axis=0)
return X_std, y_std
def transform(self, X, y):
'''
Returns min-max normalized X and y vectors.
'''
X_scaled = (X - np.min(X, axis=0))/(np.max(X, axis=0) - np.min(X, axis=0))
y_scaled = (y - np.min(y, axis=0))/(np.max(y, axis=0) - np.min(y, axis=0))
return X_scaled, y_scaled
# Gradient Descent
def train_using_gradient_descent(self, X, y, learning_rate=0.5):
'''
Train network using gradient descent.
'''
N = X.shape[0]
dJdW_for_layer, deltas_for_layer = self._derivatives_with_respect_to_weights(X, y)
for layer in sorted(self._WEIGHTS_FOR_LAYER.keys()):
W = self._WEIGHTS_FOR_LAYER[layer]
self._WEIGHTS_FOR_LAYER[layer] -= learning_rate * dJdW_for_layer[layer]
self._BIAS_FOR_LAYER[layer] -= learning_rate * np.sum(deltas_for_layer[layer], axis=0, keepdims=True)/N
self._update_db_weights_and_bias()
def forward(self, X):
'''
Propogate inputs though network.
'''
self._OUTPUT_FOR_LAYER[0] = X
for layer in sorted(self._TABLE_NAME_FOR_LAYER.keys())[1:]:
W = self._WEIGHTS_FOR_LAYER[layer - 1]
bias = self._BIAS_FOR_LAYER[layer - 1]
net = np.dot(self._OUTPUT_FOR_LAYER[layer - 1], W) + bias
self._OUTPUT_FOR_LAYER[layer] = self._sigmoid(net)
yHat = self._OUTPUT_FOR_LAYER[self._number_of_hidden_layers+1]
return yHat
def main():
net = Neural_Network(topology=commons.topology, delete_old_db=True)
if __name__ == "__main__":
main()